ENIGMA Chapter 4 – How Does the Machine Work? (Part 2)
After looking at the various elements of the Enigma machine in Chapter 4 Part 1, we will now go into a bit more detail on how the 26 letters are linked in 13 letter pairs through electrical circuits. Grasping this aspect will make it easier to understand the concept behind the Bombe, the codebreaking machine Alan Turing developed in Bletchley Park in 1939, first produced in 1940.
Examples without plugboard cables
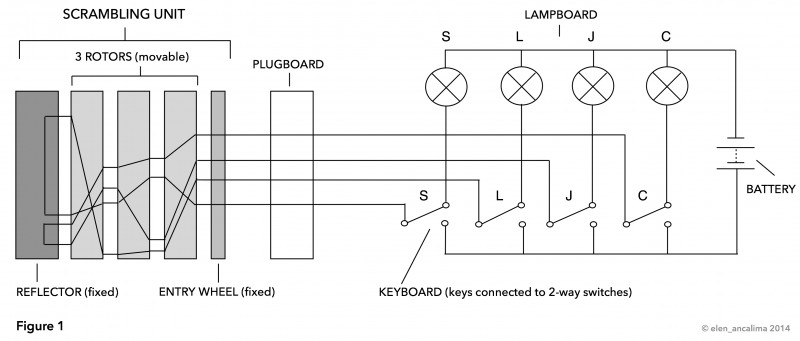
Figure 1 shows a simplified circuit diagram of the connections between 4 of the 26 keyboard keys and lamps. If no key is pressed, the circuit is broken, and electricity cannot flow.
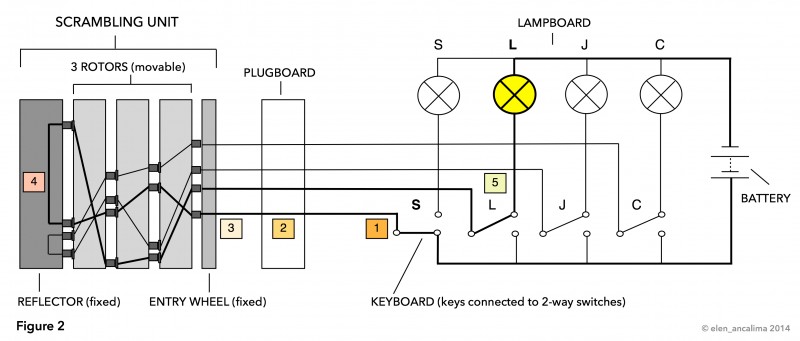
In Figure 2, a key on the keyboard has been pressed, which has closed one of the possible electric circuits (after one of more rotors moved one position).
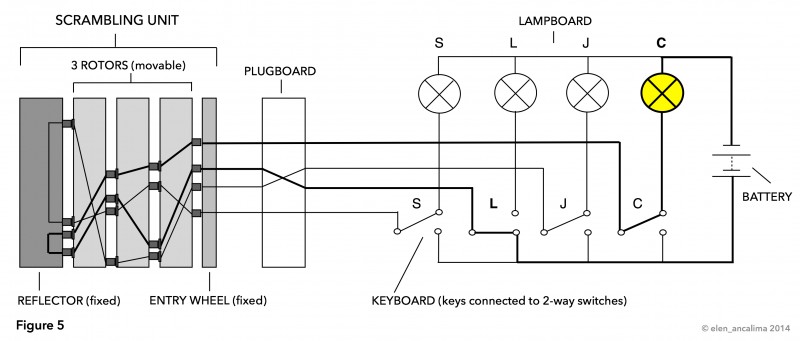
When the key for S is pressed, the 2-way switch underneath it [1] disconnects from the S lamp and makes contact with the wire coming from the battery. This closes an electrical circuit, thus current can flow from the battery through the 2-way switch [1] and the plugboard [2] to the fixed entry wheel [3]. (No plugboard cables are used in this example, so the plugboard can be ignored for the moment.)
Current enters the scrambling unit at the entry wheel [3]. It is picked up by the first rotor’s spring-loaded pin that is touching the entry wheel’s S contact. It then flows from right to left through the configuration of wires that the three rotors present at this particular setting.
Electricity enters the reflector [4] at one position, exits at another before flowing back through the three rotors, this time from left to right and on a different path of wires. It exits the scrambling unit at the entry wheel [3], flows once again through the plugboard [2] and reaches the 2-way switch for the letter L. Since the key for L is not pressed, the 2-way switch is connected with the L lamp, which lights up when current reaches it [5]. This indicates that the ciphertext replacement for the letter S is L.
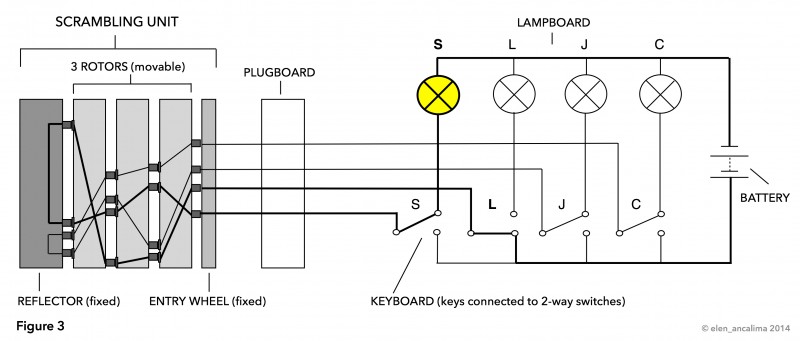
As mentioned in Chapter 3 (The Substitution Cipher), all cipher alphabets created by the Enigma machine are reciprocal due to the nature of the reflector. This means that if S is encoded by L at one setting, then L is encoded by S when the same setting is used. Figure 3 shows this scenario:
The electrical pathways in the scrambling unit for encoding L-> S and S-> L are exactly the same – the only difference being the direction of the electrical current. For codebreaking purposes it is therefore often not relevant if a letter is plaintext or ciphertext, it is only important what two letters are linked at a specific setting.
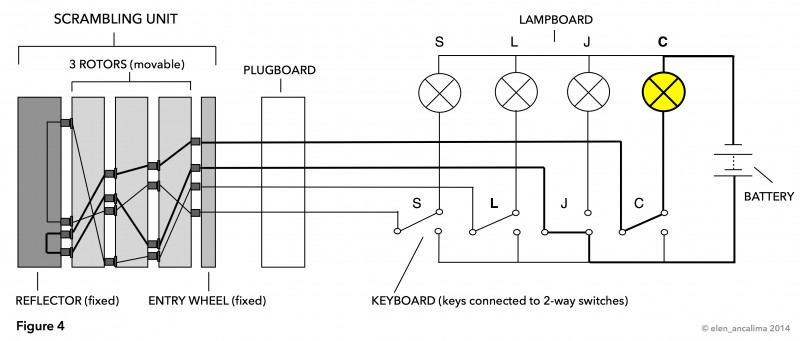
If a different key is pressed at the same setting, e.g.J in Figure 4, then a different electrical circuit is closed, in this case illuminating the C lamp.
Effect of the plugboard
In Figure 5, plugboard cables swap the letters J and L. It is important to notice that even though the lamp C now lights up when L is pressed (and not the key for J as before), the electrical pathway in the scrambling unit is the same as in Figure 4.
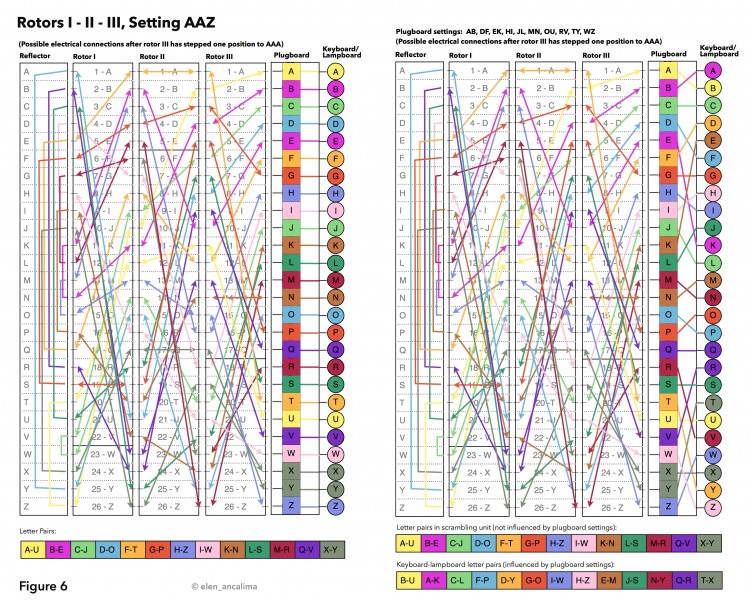
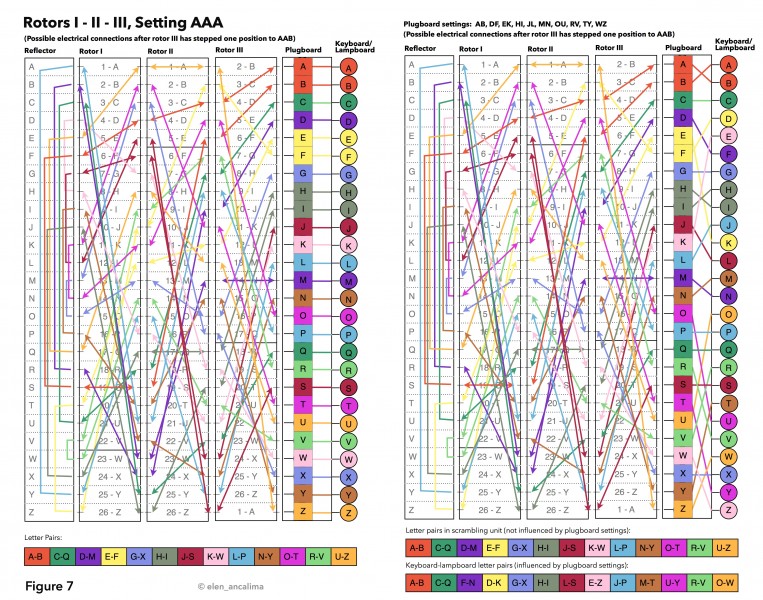
This becomes even more apparent when we look at all 13 linked letter pairs that are possible at one particular setting (initial setting AAZ in Figure 6 and AAA in Figure 7). The examples on the left don’t use the plugboard, while the ones on the right swap 20 letters with 10 cables.
The scrambling units in the left examples deliver 13 possible letter pairs (marked with different colours) – the cipher alphabet for that setting. When the plugboard doesn’t have any cables attached, the current for a specific letter flows directly through it and illuminates the corresponding lamp.
If however letters are swapped with plugboard cables, as seen in the examples on the right, then the current is diverted to a different lamp (or is diverted before it even enters the scrambling unit). The 13 letter pairs are different. BUT: the electrical pathways through the rotors and reflector are NOT AFFECTED. This fact is incredibly important when it comes to dealing with Turing’s idea behind his crucial codebreaking machine, the Bombe.
A 3-rotor Enigma machine without plugboard cables has approximately the following number of different settings (when three rotors are chosen from five possibilities):
Choice and position of rotors: 60 possibilities x
Possible rotor settings: 26 x 26 x 26 possibilities =
1,054,560 different settings
If you add 10 cables to the plugboard, the number of different possibilities becomes almost astronomical:
Choice and position of rotors: 60 possibilities x
Possible rotor settings: 26 x 26 x 26 possibilities x
10 plugboard cables, connecting 20 letters: 150,738,274,937,250 possibilities = 158,962,555,217,826,360,000 different settings.
This huge number is one of the reasons the Germans in World War II were so convinced the cipher could not be broken. What Alan Turing was able to do was figure out how to basically link several Enigma machines in a particular way so that the plugboard settings became irrelevant. In a few chapters time we will take a closer look at how the Turing Bombe mechanically searched for a particular scrambling unit setting (which is not affected by the plugboard).
This triumph of the human mind over a machine is what fascinates me the most about the Enigma story. The next chapter will show how messages enciphered by the Enigma machine were first decoded in the 1930s, due to the brilliant work of Polish cryptanalysts.
—
Next Post: ENIGMA Chapter 5 – Polish Pre-War Codebreaking Successes
Previous Posts: Chapter 1 – Historical Background, Chapter 2 – Invention of the Enigma Machine, Chapter 3 – The Substitution Cipher, Chapter 4 – How Does the Machine Work? (Part 1)
—
FURTHER READING:
Books:
SINGH, Simon. The Code Book. The Secret History of Codes and Code-Breaking. London, 1999
WELCHMAN, Gordon. The Hut Six Story. Breaking the Enigma Codes. Oxford, 1997
Websites:
CRYPTO MUSEUM: Enigma (Retrieved April 2014)
ELLIS, Claire. Plus Maths – Exploring Engima 2005 (Retrieved April 2014)
RIJMENANTS, Dirk. Cipher Machines and Cryptology. Enigma Menu (Retrieved April 2014)
SALE, Tony. Technical Specification of the Enigma (Retrieved April 2014)


Write a comment
You need to be logged in to leave a comment.